Hyperspectral imaging
Mathematical methods for innovation in medicine and industry
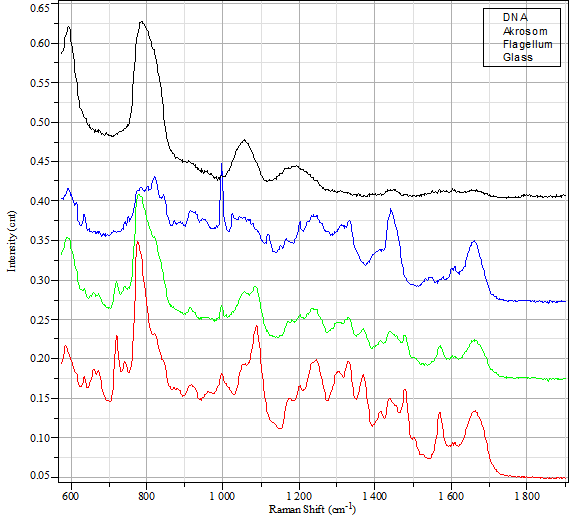
In hyperspectral imaging not just three (red, green, and blue) but thousands of so-called spectral channels are measured at each pixel of a spatially-resolved image. This allows using spectral fingerprints to recognize objects in the image, ranging from molecules in spatially-resolved Raman spectroscopy or telling streets apart from trees in satellite imagery. However, this additional information comes at the price of increased data volume, easily going into tens of gigabytes per image.
In the joint project HYPERMATH the challenge of this "big data" problem is answered from a mathematical point of view. The problem has great importance as multitudinous applications in medical technology, material testing or even movie camera development are eager to take advantage of this technique. Next-generation products require next-generation algorithms and methods.
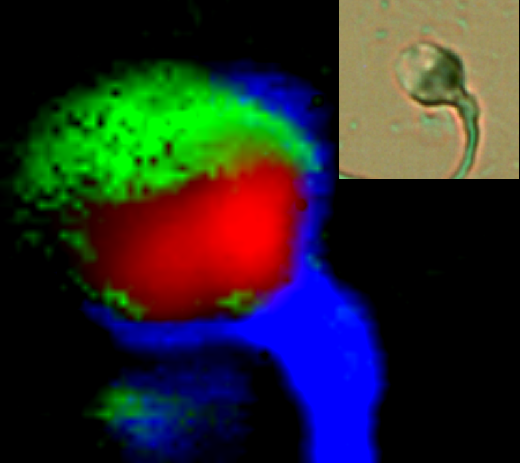
For selected partners from various high-tech areas, such as medicine, communcation, producting/material testing, a proof-of-principle is developed in cooperation with industrial partners. The work package of the University of Saarland includes the development of a stable and highly efficient solver for the mathematical optimization problems, i.e. enabling imagery in realtime. To this end, deterministic methods as sequential subspace methods and statistical methods (AG Prof. Henryk Zähle) are being employed.
For further details wer refer to the project's homepage.

